לאחרונה קראתי את ההוכחה של ארנולד שאין נוסחא לפתרון של פולינומים ממעלה 5. היא מעניינת ואני רוצה לספר עליה פה. הטיעון מתחיל בקשר בין מקדמים של פולינום לשורשים שלו וממשיך לניתוח שיטתי של איזה נוסחאות משיגות אילו קשרים.
מקדמים ושורשים
הרעיון הוא לשנות בהדרגה מקדמים של פולינומים ולראות מה יוצאים השורשים לאורך הדרך. יש אפליקציה נחמדה שמאפשרת לשנות את השורשים או את המקדמים (במישור המרוכב) ולראות מה קורה למקדמים או לשורשים בהתאמה. אחד הטריקים שאפשר לעשות, אפילו בפולינום ממעלה שניה, זה להזיז את אחד המקדמים במעגל ושהשורשים של הפולינום יתחלפו זה עם זה.
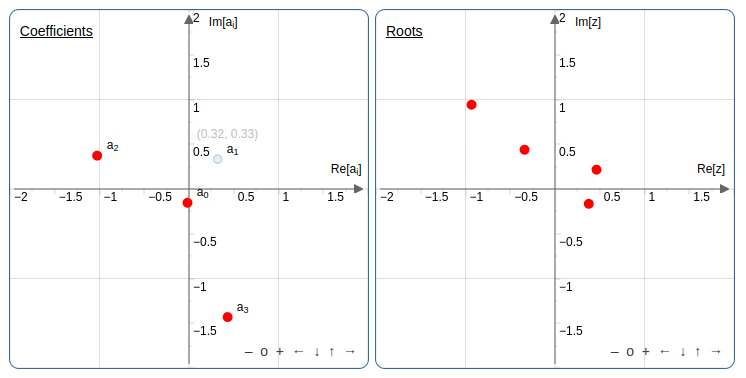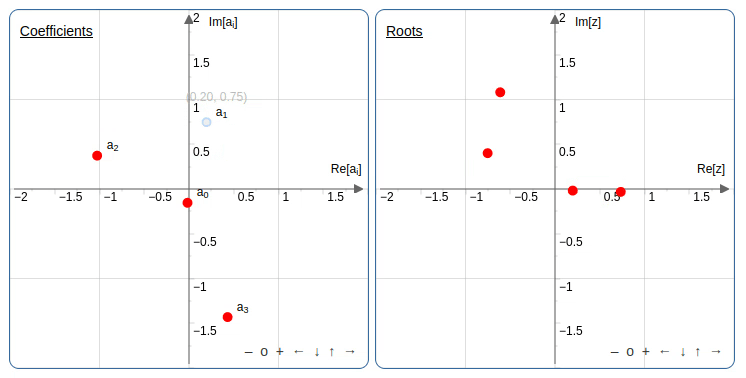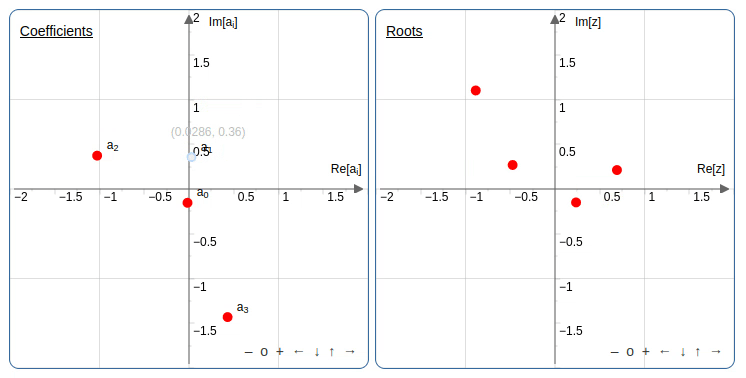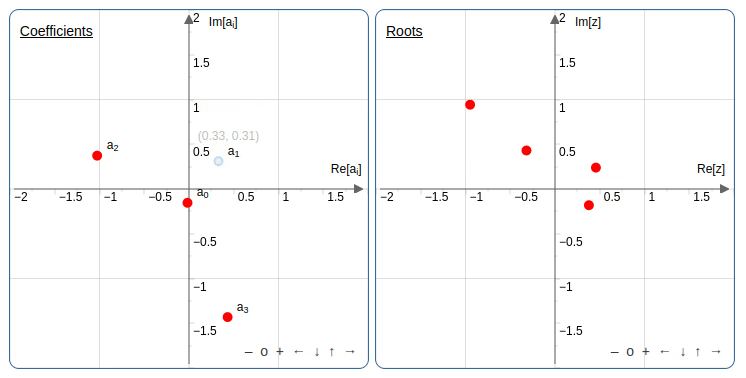
למי שרוצה לנסות באפליקציה מעלה שניה: אפשר לקבוע את המעלה מתחת למסך של השורשים.
מתנועה כזו של המקדמים, שבסופה המקדמים והשורשים חוזרים לאותו מקום אבל השורשים מחליפים מקום זה עם זה, משתמע
אין פונקציה רציפה מהמקדמים של פולינום ממעלה שנייה שנותנת שורש של הפולינום.
אילו היתה פונקציה רציפה $z(a_0, a_1)$ שתמיד נותנת שורש של הפולינום $x^2 + a_1 x + a_0$, אז כשמזיזים את $a_0$ או $a_1$ במסלול מעגלי התמונה $z$ היתה זזה גם היא במסלול שחוזר לנקודת ההתחלה. אבל כמו שראינו שורשים לא מתנהגים ככה.
איך זה מסתדר עם הנוסחא שלומדים בבית ספר $ x_{1,2} = \tfrac{-b \pm \sqrt{b^2 – 4ac}}{2a} $? הביטוי $\sqrt{\cdot}$ הוא לא פונקציה רציפה במספרים המרוכבים. ואפשר להסיק שלא קיימת פונקציה שמשתמשת רק בפעולות רציפות כמו חיבור, חיסור, כפל, חילוק, סינוס וקוסינוס, אקספוננט, וכו' ששקולה לאותו ביטוי, או שמחשבת שורשים של פולינומים בדרך אחרת.
שורש רציף
יש מובן שבו פונקציית השורש דווקא רציפה: אם מזיזים מספר מרוכב באופן רציף, למשל לאורך מסילה $\gamma : [0, 1] \to \mathbb{C}$, אז יש לו שורש רציף, כלומר מסילה $\sqrt{\gamma} : [0, 1] \to \mathbb{C}$ שמקיימת $\gamma(t) = \left( \sqrt{\gamma}(t) \right)^2$ לכל $t$. בדרך כלל יש שתי אפשרויות למה $\sqrt{\gamma}$ יכולה להיות, עם סימן הפוך זו מזו. אבל בכל פעם ש-$\gamma$ עוברת ב-$0$ השורש הרציף $\sqrt{\gamma}$ יכול להחליף סימן וזה מכפיל את כמות האפשרויות.
אין במרוכבים פונקציית שורש רציפה ולכן אפשרי שהמסילה $\gamma$ מעגלית ו-$\sqrt{\gamma}$ לא. הדוגמא הכי פשוטה היא $\gamma(t) = e^{i\tau t}$, כאשר נסמן כמקובל $\tau = 2\pi$. אם המסילה $\sqrt{\gamma}$ לא מעגלית אז היא נגמרת בסימן הפוך $\sqrt{\gamma}(1) = -\sqrt{\gamma}(0)$.
לאילו מסילות מעגליות $\gamma$ נוכל לדעת שהמסילה $\sqrt{\gamma}$ גם כן מעגלית? או ליתר דיוק שתהיה מסילת שורש מעגלית, כי הרי כל הבעיה היא שיש כמה שורשים לכל מספר. דרך אחת להשיג את זה היא ללכת לאורך מסילה כלשהי, ואז את כל המסילה בכיוון ההפוך. נסמן את זה $\gamma \ \overline{\gamma}$. למסילה מהצורה הזו יש שורש שהוא מסילה מעגלית. גם אם נלך לאורך מסילה פעמיים $\gamma \ \gamma$ אפשר לבחור שורש רציף של זה שיהיה מעגלי: אם $\sqrt{\gamma}$ לא הופכת סימן אז חוזרים על אותו מסלול שוב, ואם היא הופכת סימן אז בחצי השני של $\sqrt{\gamma \ \gamma}$ בוחרים סימן הפוך ואז חוזרים לנקודת ההתחלה.
קומוטטורים
הטריק של לחזור על המסילה פעמיים עובד לשורש שני, אבל לא לשורש שלישי או גבוה יותר. כדי לנתח שורשים כלליים נצטרך מגוון רחב יותר של מסילות לעבוד איתן, והסוג שגם מגוון מספיק וגם מוגבל מספיק בשביל להוכיח תכונות שלו הוא קומוטטורים. אלה מסילות מהצורה $ \gamma_1 \ \gamma_2 \ \overline{\gamma_1} \ \overline{\gamma_2} $ כאשר $\gamma_1, \gamma_2$ מסילות מעגליות.
לקומוטטור של שתי מסילות תמיד יש שורשים רציפים מכל סדר.
איך מוצאים שורש רציף של הקומוטטור שהוא מסילה מעגלית? נשתמש בשורשים של המסילות $\gamma_1$ ו-$\gamma_2$. נסמן את נקודת ההתחלה של $\sqrt[n]{\gamma_1}$ ב-$z$, שמקיים $z^n=\gamma_1(0)$. המסילה הזו מסתיימת ב-$\sqrt[n]{\gamma_1}(1) = e^{ik\tau/n}z$ עבור k שלם כלשהו. משם המסילה $\sqrt[n]{\gamma_2}$ מתחילה, והיא מסתיימת ב-$e^{i(k+m)\tau/n}z$ עם m שלם כלשהו. אז אפשר לנוע לאורך $\overline{e^{im\tau/n}\sqrt[n]{\gamma_1}}$ ולהגיע ל-$e^{im\tau/n}z$, והמסילה $\overline{e^{-ik\tau/n}\sqrt[n]{\gamma_2}}$ תחזיר אותנו ל-$z$. כלל הצעדים האלה מתארים מסילה מעגלית שהיא שורש $n$-י של הקומוטטור $ \gamma_1 \ \gamma_2 \ \overline{\gamma_1} \ \overline{\gamma_2} $.
מזה נובע שביטוי שיש בו כמות בלתי מוגבלת של פעולות רציפות, וסימן שורש אחד, יחזור לאותו ערך כשהולכים לאורך מסילה שהיא קומוטטור של שתי מסילות. למעשה כך גם ביטוי עם שני סימני שורש שלא מעורבבים זה עם זה כמו $\sqrt{x} + \sqrt[4]{y}$.
משוואות ממעלה שלישית
במרחב הפולינומים ממעלה 3 יש מסלול שהוא קומוטטור של שני מעגלים, ועדיין לא מעביר את כל השורשים חזרה לאותו מקום בסוף. אפשר למצוא יחסית בקלות פולינום ושני מעגלים שישיגו את שני סוגי הערבוב $\gamma_1$ ו-$\gamma_2$ כמו בדיאגרמה הזו:
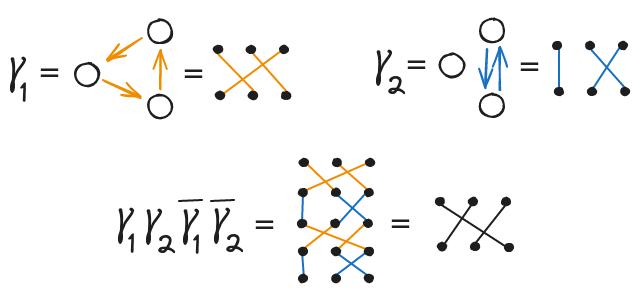
בתנועה לאורך המסילה $ \gamma_1 \ \gamma_2 \ \overline{\gamma_1} \ \overline{\gamma_2} $ כל ביטוי שיש בו רק שורש פשוט יחזור לאותה הנקודה, בעוד ששורש של הפולינום יעבור למקום אחר. ולכן
בנוסחא לפתרון פולינומים ממעלה 3 שיש בה רק פונקציות רציפות ושורשים, חייב להיות שורש בתוך שורש.
במקרה יש גם נוסחא כזו: הפתרון של $x^3 + ax + b = 0$ הוא
$ x = \sqrt[3]{-\tfrac{1}{2}b+\sqrt{\tfrac{1}{4}b^2+\tfrac{1}{27}a^3}} $ $ + \sqrt[3]{-\tfrac{1}{2}b-\sqrt{\tfrac{1}{4}b^2+\tfrac{1}{27}a^3}} $
מה קורה פה? ביטוי כמו $z=-\tfrac{1}{2}b+\sqrt{\tfrac{1}{4}b^2+\tfrac{1}{27}a^3}$ שמחושב מהמקדמים משתנה כאשר מזיזים את המקדמים. אפשרי להזיז את המקדמים במסלול מעגלי וש-$z$ לא יחזור לאותו ערך, אבל במסלול שהוא קומוטטור הוא כן יחזור לאותו ערך, כלומר יסגור מעגל. זה אומר שביטוי כמו $\sqrt[3]{z}$ ינוע במסלול מעגלי כאשר המקדמים נעים במסילה שהיא קומוטטור של קומוטטורים. בתמורות על 3 איברים אפשר לחשב את כל הקומוטטורים של קומוטטורים, והם תמיד תמורת הזהות. לכן אין סתירה ברציפות לזה שביטוי כמו $\sqrt[3]{z}$ יהיה הנוסחא לשורשי משוואה ממעלה שלישית. אילו היה קומוטטור של קומוטטורים שאינו תמורת הזהות, היינו יודעים שעם הזזת המקדמים לאורך המסילה המתאימה גם $\sqrt[3]{z}$ יחזור לאותו ערך, וזה לא קורה בבחירה רציפה של אחד השורשים של המשוואה.
משוואות ממעלה חמישית
אם משחקים באפליקציה עם פולינומים ממעלות גבוהות, בדרך כלל קל למצוא שינויים במקדמים שיחליפו קבוצה גדולה של שורשים, וקצת יותר קשה למצוא שינויים שיחליפו שני שורשים בלבד, ועוד יותר קשה להשיג תמורה כרצוננו. אבל עדיין אפשר.
בהזזה מעגלית של המקדמים אפשר להחליף בין המקומות של השורשים בכל התמורות.
דרך אחת להבין למה: בהינתן שורשים $z_1, z_2, \ldots, z_n$ המקדמים של הפולינום
$ x^n + a_{n-1}x^{n-1} + \ldots + a_1 x_1 + a_0 x_0 $ $ = (x-z_1)(x-z_2)\cdots(x-z_n) $
הם פונקציות רציפות של השורשים $a_i(z_1, \ldots, z_n)$. לכן כל תבנית הזזה של השורשים משתקפת במסלול שכל המקדמים נעים ביחד במרחב המקדמים. ולכן אפשר היה ליצור אותה באמצעות הזזה של המקדמים באותו מסלול.
במעלה חמישית יש יותר שורשים, ויותר תמורות עליהם. כמו שהסברנו למעלה, או בניסוי וטעיה למי שאוהבת להתנסות, אפשר להשיג את כל $5!=120$ התמורות על 5 איברים בהזזה של המקדמים של הפולינום במסלול מעגלי. בפרט, כמו במעלות 2 ו-3 אין נוסחא רציפה לשורשים, וכמו במעלה 3 יש קומוטטורים שיוצרים תמורה לא טריוויאלית של השורשים, ולכן בנוסחא עם פונקציות רציפות ושורשים בלבד יהיה חייב להיות שורש בתוך שורש.
אם מחשבים את כל $120^2$ הקומוטטורים, רואים שמקבלים בסך הכל $60$ תמורות. אם מחשבים את כל $60^2$ הקומוטטורים שלהן מקבלים שוב את אותן $60$ תמורות, האוסף שבדרך כלל נקרא $A_5$. כלומר הגענו למצב שיש קומוטטור של קומוטטור שאינו תמורת הזהות על השורשים. זה אומר שביטוי עם שורש בתוך שורש, אם מנסים לפרש אותו באופן רציף כשהמקדמים משתנים, לא יכול לתת שורש של הפולינום. אבל אחרי שהגענו לקבוצת הקומוטטורים $A_5$ חישוב של קומוטטורים שוב ישאיר אותנו עם מלוא הקבוצה $A_5$, ולכן גם שורש בתוך שורש בתוך שורש לא יתן ביטוי שאפשר להשתמש בו כנוסחא לשורשי משוואה ממעלה חמישית, וכן הלאה לכל כמות סופית של שורשים בביטוי. ולסיכום
אין ביטוי עם פעולות חשבון, פעולות רציפות אחרות או שורשים שנותן פתרון של משוואה כללית ממעלה חמישית.
עוד
ההוכחה הזו פתחה דרך לתיאוריה שמקשרת טופולוגיה לפולינומים ולתורת השדות. אבל הבסיס, תורת גלואה, עדיין חשוב יותר. זה התחום שעוסק בחקר והבנה מעמיקים הרבה יותר של פולינומים, שורשים והמשמעות של פעולות החשבון. גדי אלכסנדרוביץ' כתב הצגה יפה של הנושא באביב-קיץ 2018 ואני ממליץ עליה מאוד.
כדאי לומר גם שכדי לחשב שורש חמישי, כלומר למצוא את הספרות שלו, צריך להשתמש בטכניקות שעובדות באותה המידה לפתור כל משוואה ממעלה חמישית, וגם למעלות גבוהות יותר. עדיין מעניין לדעת איזה פונקציות מאפשרות לפתור איזה משוואות, ויש מחקר פעיל בתחום. יש גם תוצאות מעניינות ספציפית לגבי מעלה חמישית, עם קשרים לגיאומטריה יוונית ולגיאומטריה מודרנית.
