אחרי הפוסט הקודם, ובעקבות הערות הקוראים, הסתכלתי איפה הנושא התחיל ואיך. ונראה שהשאלה של קצב גידול של חבורות עלתה בעקבות פופולריזציה די אגרסיבית של מילנור בסביבות שנת 1968, בה הוא ומתמטיקאים שעובדים איתו פרסמו את השאלה בכמה ז'ורנלים שונים ופרסמו הוכחות חלקיות למשפט שבו פתחנו בפוסט הקודם.
מלכתחילה נראה שאת חלק מהאנשים שבתה עצם היכולת "לעשות קומבינטוריקה" מסוג חדש על קבוצות היוצרים של חבורות, והם אהבו את העבודה על החבורות עצמן ועל גרף קיילי. ובחלק מהמאמרים היו תוצאות בגאומטריה רימנית שהראו שקצב הגידול של החבורה היסודית קשור לתכונות גאומטריות של המרחב, מה שמרחיב תוצאות שהיו ידועות קודם על קשר בין תכונות אלגבריות של החבורה היסודית לבין גאומטריה של המרחב. זה מתקשר טוב במיוחד כי המשפט (או ההשערה בשלב זה, כי הוא הוכח רק בשנת 1981) מקשר בין קצב גידול של חבורה לבין תכונות אלגבריות שלה.
לי לא ישבו טוב המושגים בפסקה הקודמת כשהתחלתי לעלעל במאמרים האלה, אז אני אעבור עליהם פה בקצרה. המתמטיקה שמופיעה פה היא מתחומים אחרים ולא קשורה להוכחה של המשפט, ואפשר לדלג על הפוסט הזה כשקוראים את הסדרה.
ליריעה רימנית יש כמה הגדרות, וחלק מהקסם של התחום הוא שהן שקולות. ההגדרה ה"חיצונית" אומרת שמדובר בתת-קבוצה חלקה עם מימד נמוך יותר משל המרחב שהיא נמצאת בו, כמו למשל פני השטח של כדור או היפרבולואיד במרחב 3-ממדי (חלקה במובן שכל חתיכה קטנה מוגדרת באופן פרמטרי עם פונקציה גזירה). ההגדרה ה"פנימית" מדברת על קבוצה כללית, שמכוסה על ידי אוסף מפות שבכל אחת מהן יש קורדינאטות, וביחד הן מכסות את כלל היריעה, יחד עם כלל שאומר איך להתאים מפות סמוכות זו לזו בחלק החופף. זה באנלוגיה לאיך שמפות באטלס מודפס מכסות את כלל פני השטח של כדור הארץ.
תכונה מרכזית בגאומטריה רימנית היא עקמומיות, שמתארת כמה היריעה רחוקה מלהיות שטוחה, כמו שקשה יותר לעטוף כדור באריזת מתנה מאשר ספר. יש כמה מדדים לעקמומיות, אבל יש להם דבר אחד במשותף: כיווני העקמומיות יכולים להיות עם אותו סימן או בסימנים הפוכים (במדד עקמומיות שהוא המכפלה של אלה, הסימן עובר מחיובי לשלילי). למשל, אם נמצאים בנקודה הכי גבוהה על כדור, העקמומיות של המשטח בכל הכיוונים היא כלפי מטה. אבל אם מסתכלים סביב המותן של ההיפרבולואיד, כיוון עקמומיות אחד הוא פנימה, סביב ההיקף, וכיוון אחד הוא החוצה, זה שעולה למעלה ויורד למטה.
העקמומיות משפיעה על הקשר בין אורך, זווית, ונפח. איפה שכל כיווני העקמומיות זהים, סכום הזוויות במשולש קטן יהיה 180 מעלות או יותר. ואם יש כיווני עקמומיות שונים סכום הזוויות יכול להיות קטן מ-180 מעלות. גם שטחים של עיגולים או נפחים של כדורים ביריעה מתנהגים בהתאם לעקמומיות, אם העקמומיות חיובית אז הנפח של כדור קטן יותר מזה של כדור עם אותו רדיוס במרחב אוקלידי רגיל מאותו ממד. ואם העקמומיות שלילית, נפח של כדור יכול לגדול כמו פונקציה מעריכית של הממד.
מושג מרכזי אחר בגאומטריה ובטופולוגיה הוא החבורה היסודית. מדובר בדרך לקטלג את המסלולים הסגורים שקיימים במרחב, כאשר מסלולים דומים נחשבים באותה קטגוריה. למשל במשטח עם חור, כל מסלול שלא מקיף את החור אפשר לכווץ לנקודה. ומסלול שמקיף את החור דווקא אי אפשר. לכן יש יותר מקטגוריה אחת. למה קוראים לזה חבורה? מגדירים את הפעולה בתור ללכת לאורך מסילה אחת, ואז ללכת לאורך השניה. קצת מחשבה מראה שאם המסילות הן עם כיוון מוגדר, החבורה היסודית יוצאת בדיוק המספרים השלמים במקרה הזה.
מרחב קלאסי נוסף הוא הטורוס. בלי להיכנס להוכחה מדויקת, יש שני סוגים של עקומות לא-ניתנות לכיווץ, כאלה סביב החור המרכז וכאלה סביב היקף הטבעת. והן מתחלפות, במובן ששני מסלולי ההרכבה האפשריים (האחת ואז השניה, או השניה ואז הראשונה) הם מאותה מחלקה, כי אפשר להזיז באופן רציף ממסלול אחד לשני. לכן החבורה היסודית היא החבורה החילופית החופשית עם שני יוצרים $\mathbb{Z}^2$.
עוד דוגמא לחבורה יסודית היא של הטורוס עם שני חורים. פה אפשר ללכת סביב כל אחד מהחורים, ואי אפשר לעשות הזזה רציפה של העקומה שמשנה את סדר המעבר סביב החורים. במילים אחרות, החבורה היסודית אינה חילופית. וליתר דיוק היא מכילה את החבורה החופשית עם שני יוצרים שעלתה בפוסט הקודם.
מושג נוסף מעולם הטופולוגיה שעוזר להבין את החבורה היסודית הוא מרחב הכיסוי האוניברסלי. לכל יריעה רימנית יש יריעה אחרת שמדמה אותה בכל אזור אבל יותר גדולה: כלומר, קיימת העתקה שהיא איזומטריה מקומית (משמרת מרחקים קטנים) ממרחב הכיסוי למרחב שבו עוסקים. ובנוסף מרחב הכיסוי הזה הוא פשוט-קשר, כלומר שכל עקומה בו ניתנת לכיווץ, או במילים אחרות בחבורה היסודית שלו יש רק איבר אחד.
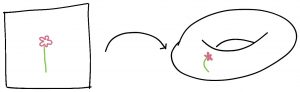
בתור דוגמא למרחב כיסוי נסתכל על הטורוס: אם בוחרים ייצוג פשוט שלו $S^1 \times S^1 \subset \mathbb{R}^4$, הוא יוצא לחלוטין ללא עקמומיות. ואז המישור הוא מרחב כיסוי שלו. כל נקודה בטורוס מכוסה על-ידי אינסוף נקודות במישור, ויש איזומטריות של המישור שמעבירות בין כל הנקודות במישור שמכסות אותה נקודה בטורוס. אלה בדיוק הזזות בכפולה של היקף המעגל בכל אחד מהצירים, ואת אלה אפשר לזהות עם איברי $\mathbb{Z}^2$.
באופן כללי, למרחב הכיסוי האוניברסלי יש את חבורת תמורות הכיסוי (לא מצאתי תרגום למונח Deck transformation אז נלך על זה), שהן איזומטריות שמשמרות את הכיסוי. והחבורה הזו תמיד איזומורפית לחבורה היסודית של המרחב המקורי.
איך כל זה קשור לקצב גידול של חבורות? הרעיון הוא לקשר בין עקמומיות של יריעות לבין אופי החבורה היסודית שלהן.
למשל, אם יריעה היא עם עקמומיות אי-שלילית בכל מקום, כלומר כמו כדור או גליל או מישור, כל הכיוונים שהמרחב "מתעקם אליהם" הם באותו צד, אז הגידול של החבורה היסודית הוא פולינומיאלי. מדוע? נבחר נקודה $x$ ביריעה ונסתכל במרחב הכיסוי האוניברסלי. ניקח נקודה $\bar{x}$ שמכסה את $x$ וקבוצת יוצרים $g_1, …, g_\ell$ לחבורת תמורות הכיסוי. נסמן ב-$m = \max_i d(g_i(\bar{x}), \bar{x})$ את המרחק המקסימלי שאחת מהן מעבירה את $\bar{x}$. מאי-שיוויון המשולש, מילה באורך $s$ מעבירה את $\bar{x}$ למרחק $sm$ לכל היותר. כלומר כדור $B_{sm}(\bar{x})$ מכיל כמות נקודות שמכסות את $x$ שגדולה לפחות כמו כדור ברדיוס $s$ בגרף קיילי של החבורה היסודית. ניתן לבחור $\varepsilon > 0$ כך שהכדורים $B_\varepsilon(g(\bar{x}))$ זרים, ולכן הגידול של החבורה היסודית חסום על-ידי קצב גידול של נפח כדור כפונקציה של הרדיוס במרחב הכיסוי. כפי שציינו למעלה, זה פולינומיאלי ביריעות עם עקמומיות חיובית.
זה היה תקציר הוכחה מאוד מתומצת, אפשר למצוא עוד פירוט במאמר המקורי. עוד אפשר למצוא שם הוכחה (בשיטה דומה) שביריעה קומפקטית עם עקמומיות שלילית בכל מקום, החבורה היסודית היא עם גידול מעריכי. ודוגמא ליריעה עם עקמומיות שלילית שאינה קומפקטיות והגידול של החבורה היסודית הוא פולינומיאלי.
תוצאה קלאסית מטופולוגיה אומרת שכל חבורה ניתנת למימוש כחבורה יסודית של יריעה כלשהי. אם יש קישור בין תכונות אלגבריות של חבורה לבין קצב הגידול שלהן, ובין קצב הגידול לבין הגאומטריה של המשטח, זה עשוי לאפשר לחקור שאלות באלגברה מופשטת באמצעים של גאומטריה רימנית. ובכיוון ההפוך, הרבה פעמים תכונות של הטופולוגיה (כמו החבורה היסודית) ידועות יותר טוב מאשר הגאומטריה של אובייקטים מעניינים, ואולי בעזרת תכונות של החבורות האלה אפשר להגיע למסקנות לגבי הגאומטריה. זו יכולה להיות מוטיבציה לעסוק בקצב גידול של חבורות.

הבנתי! בעיקר את הציורים🤔