תורת החבורות הגאומטרית

שמעתי על תורת החבורות הגאומטרית בסמינר של יהודה שלום, בו הוכחנו משפט שכבר במבט ראשון נראה יפהפה, אפילו בלי להכיר את התחום מסביב. ואני עדיין לא מכיר בו כלום מעבר למה שהיה באותו סמינר. בקצרה, המשפט אומר

חבורה נוצרת סופית היא עם קצב גידול פולינומאלי אם ורק אם יש לה תת-חבורה נילפוטנטית מאינדקס סופי

התכנית לסדרת הפוסטים הזו היא להוכיח את המשפט. אז נתחיל, ונראה איזה דברים מעניינים נפגוש בדרך.

בפוסט הזה נסתכל על כמה דוגמאות ונציג את המונחים שמופיעים במשפט.

אם $G$ חבורה עם קבוצת יוצרים $S$, גרף קיילי שלה הוא גרף מכוון שהקודקודים שלו הם האיברים $g \in G$ והקשתות הן $ g \curvearrowright g \cdot s $ לכל $s \in S$. לדוגמא, אם $G$ חבורת הסימטריות על $\{1,2,3\}$ ו-$S = \{(12), (123)\}$, הגרף הוא

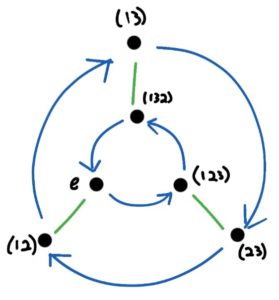
בתורת החבורות הגאומטרית עוסקים בתכונות של גרף קיילי כמרחב מטרי. בשביל זה צריך שהגרף לא יהיה מכוון, ולכן קבוצות היוצרים שנתעסק איתן יהיו קבוצות יוצרים סימטריות, כלומר שמכילות גם את כל האיברים ההפכיים, או $ S = S^{-1} $.

דוגמא לתכונה מטרית היא שלגרף הזה יש הרבה איזומטריות: לכל $g \in G$, ההעתקה $x \mapsto g \cdot x $ היא איזומורפיזם של הגרף. למשל, $f_1(x) = (13) \cdot x$ לוקחת את הקשת $e \curvearrowright (12)$ לקשת $(13) \curvearrowright (132)$. כהערת אגב, נשים לב שסדר האיברים משנה כי החבורה אינה חילופית: ההרכבה בכיוון ההפוך $f_2(x) = x \cdot (13)$ אינה איזומורפיזם, היא לוקחת את הקשת $e \curvearrowright (12)$ ללא-קשת $(13) \not \curvearrowright (123)$.

אותנו תעניין כמות האיברים בכדור בתלות ברדיוס, למשל סביב הראשית (בגלל האיזומורפיזמים לא משנה מה מרכז הכדור). ונעסוק רק בחבורות בנות מניה עם קבוצת יוצרים סופית.

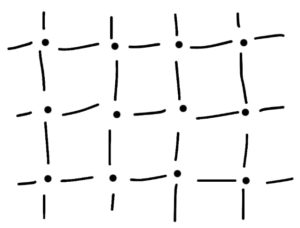
בתור דוגמא לחבורה נוצרת סופית ניקח את החבורה החיבורית $\mathbb{Z}^2$ (החבורה האבלית החופשית עם שני יוצרים). הנה גרף קיילי שלה עם קבוצה היוצרים $S_1 = \{\pm (1,0), \pm (0, 1)\}$:

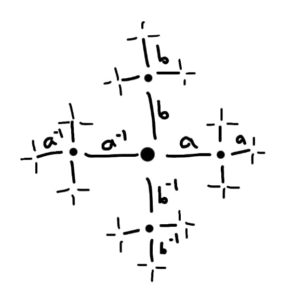
עוד דוגמא לחבורה נוצרת סופית היא החבורה החופשית עם שני יוצרים $ F_2 = \langle a, b \rangle$:

כל חבורה נוצרת סופית חייבת להיות בת מניה, אבל ההיפך לא נכון, למשל החבורה החיבורית של $\mathbb{Q}$ אינה נוצרת סופית: אם $ \frac{m_1}{n_1}, …, \frac{m_r}{n_r} \in \mathbb{Q} $ אז את כל הסכומים וההפרשים שלהם אפשר לרשום עם מכנה $\text{lcm}(n_1, …, n_r)$.

כמה איברים יש בכדור ברדיוס $r$ בכל חבורה? עבור $\mathbb{Z}^2$ אפשר לחשב ולקבל $2r^2 + 2r + 1$. עבור $F_2$ המספר הוא $2 \cdot 3^r – 1$.

ביטוי אחד יצא פולינומיאלי והשני יצא מעריכי. למה זה? ובכן, כדור בגרף של $\mathbb{Z}^2$ מוכל בריבוע במישור, ולכן מכיל נקודות במישור לפי גודל הריבוע, שהוא פולינום מדרגה 2. מצד שני, בגרף קיילי של $F_2$ אין מעגלים בכלל, ולכן אם כל קודקוד הוא מדרגה גבוהה מ-2 (ובגרף קיילי כל הקודקודים תמיד מאותה דרגה), הגידול חייב להיות מעריכי.

את הטיעונים האלה אפשר להכליל באיזושהי מידה. נתחיל מ-$\mathbb{Z}^2$ עם קבוצת יוצרים אחרת: $ \{ \pm(1,0), \pm(3,1), \pm(1,-3) \} $

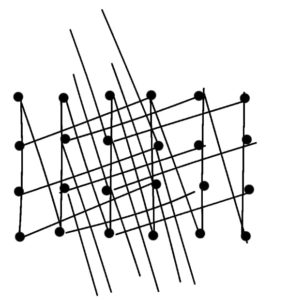
כל יוצר מעלה או מוריד עד 3 בכל קורדינאטה, ולכן ביטוי שמכיל $n$ יוצרים יוצא נקודה בתוך הריבוע $[ -3n, 3n] \times [-3n, 3n]$, ויש רק $(6n+1)^2$ נקודות שלמות כאלה.

באופן מעט יותר כללי, אם גידול של חבורה (כלומר נפח כדור בגרף קיילי כפונקציה של הרדיוס) הוא פולינומיאלי בקבוצת יוצרים אחת, הוא כזה גם בכל קבוצת יוצרים סופית אחרת. נניח שבגרף קיילי של $(G,S_1)$ נפח של כדורים מקיים $|B_{S_1}(r)| \le A r^B$. אם $S_2$ קבוצת יוצרים סופית אחרת, כל איבר ב-$S_2$ ניתן להציג כביטוי באיברים של $S_1$. אם הביטוי הארוך מבין אלה הוא באורך $m$ אז $B_{S_2}(r) \subset B_{S_1}(m\cdot r)$, ולכן $|B_{S_2}(r)| \le A m^B r^B$.

קל גם לראות שהגידול של כל חבורה חילופית נוצרת סופית הוא פולינומיאלי: לפי משפט המבנה לחבורות חילופיות נוצרות סופית כל חבורה הזו היא מכפלה ישרה של $\mathbb{Z}^d$ וחבורה סופית. החבורה $\mathbb{Z}^d$ היא עם גידול פולינומיאלי מאותה סיבה כמו $\mathbb{Z}^2$, והחלק הסופי לא משנה את סדר הגודל של הגידול אלא רק את הגורמים הקבועים.

אבל יש גם חבורות לא חילופיות עם גידול מסדר פולינומיאלי. הדוגמא שראינו בקורס היא חבורת הייזנברג. לא נוח להציג אותה גרפית ולא קל להתרשם מקצב הגידול שלה, אבל מחיפוש מהיר באינטרנט נראה שזו הדוגמא הפשוטה ביותר לחבורה עם גידול פולינומיאלי שאינה חילופית (עד-כדי חלק סופי). איברי החבורה הם שלשות של מספרים שלמים, עם הפעולה

$$ (a, b, c) \circ (d, e, f) = (a+d, b+af+e, c+f) $$

ונפח כדור בגרף קיילי פרופורציוני לחזקה הרביעית של הרדיוס. לא נראה לי ששווה לחזור פה על החישובים, מי שרוצה יכולה לבדוק לבד.

בכל מקרה, עולה השאלה לאיזו חבורה יש איזה קצב גידול. וההפרדה הראשונה, בין סדרי הגידול הפולינומיאליים לבין כל הקצבים המהירים יותר, קשורה לתכונה אלגברית לחלוטין של החבורה: שהיא (עד-כדי אינדקס סופי) נילפוטנטית. להבנתי יש גם גרסא כמותית של המשפט, שמקשרת בין סוג הנילפוטנטיות לבין המעריך של הפולינום. ויכול להיות שיש עוד מחקר לגבי חבורות עם גידול שהוא בין פולינום ופונקציה מעריכית, או אם יש קצבי גידול מעריכיים עם בסיס שמתחלף הלוך ושוב בין כמה ערכים. הכל נשמע כמו המשכים טבעיים אבל אני לא מכיר את התחום בכלל.

מה זה חבורה נילפוטנטית? זו תכונה שמכלילה חילופיות, ולכן כדי לתאר אותה משתמשים בקומוטטור. זו פעולה על שני איברים ש"מודדת" כמה הם לא מתחלפים: אם $a,b \in G$, הקומוטטור שלהם מוגדר כ-$[a, b] = a^{-1}b^{-1}ab$. אם האיברים מתחלפים אז $[a,b]=e$, ואם החבורה חילופית אז $[G,G]=\{e\}$. חבורה נקראת נילפוטנטית אם קורה אותו דבר עם צירוף יותר ארוך של קומוטטורים: אם כל הצבה בביטוי $[\cdot, [\cdot, [\cdot, \cdot]]]$ עם עומק קבוע כלשהו, גדול כרצוננו אך לא תלוי בהצבה, יוצאת איבר היחידה.

ולמה השתרבב למעלה "עד-כדי אינדקס סופי"? כדי לטפל במקרים כמו $ G = \mathbb{Z} \times A_5$, כאשר $A_5$ חבורת התמורות הזוגיות מסדר 5. לזו יש תכונה שכל איבר בחבורה הוא קומוטטור של זוג איברים מהחבורה. לכן $G$ אינה נילפוטנטית, ועדיין קצב הגידול שלה הוא לינארי.

אז המשפט אומר שבהינתן חבורה נוצרת סופית, השאלה אם הגידול של כדורים בגרף קיילי הוא מסדר גודל פולינומיאלי או יותר מכך, שקולה לשאלה אם לחבורה יש תת-חבורה נילפוטנטית מאינדקס סופי.

בפוסטים הבאים נוכיח את המשפט, ניתן עוד דוגמאות, ואולי נחקור חבורות מדרג ביניים עם גידול בין פולינומיאלי למעריכי.