ריצוף של המישור הוא תחום פעיל בהנדסה, באמנות ובמחשבה האנושית מראשית ההיסטוריה. בשפה מתמטית, ריצוף של המישור עם אריח $ A \subset \mathbb{R}^2 $ הוא אוסף של עותקים של האריח, שביחד מכסים את כל המישור ואין ביניהם חפיפות, עד-כדי קבוצות ממידה 0. העותקים יכולים להיות הזזות, סיבובים, או שיקופים. מדברים גם על ריצוף באמצעות קבוצה של אריחים ולא רק אריח אחד, או על ריצוף שמכסה את המישור ב-$k$ שכבות, גם אם אף קבוצה חלקית שלו לא מכסה את המישור בשלמות פעם אחת. ויש מחקר גם על ריצוף של מרחבים אחרים, כמו מרחב מממד גבוה יותר, או הספירה והמישור ההיפרבולי.
התעניינתי לאחרונה בשאלת המחזוריות של ריצופים, אספר פה מה למדתי.
ההגדרה של מחזור של ריצוף היא הזזה שמשמרת את אוסף העותקים של האריח. קל לראות שזו תת חבורה דיסקרטית של החבורה החיבורית $\mathbb{R}^2$. אם הדרגה שלה היא 2, אומרים שהריצוף מחזורי. יש אריחים שאפשר לרצף איתם את המישור באופן מחזורי בלבד, ויש אריחים שאפשר לרצף איתם באופן לא מחזורי. ויש אריחים שלא ניתן לרצף את המישור איתם בכלל.
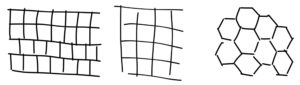
עם משושים ניתן לרצף את המישור רק באופן מחזורי. למה? אם מסתכלים מה קורה ליד קודקוד של אחד המשושים, רואים שצריך להשלים עוד זווית של 240°, וזמינות לנו רק זוויות של 120° מקודקודים של משושים אחרים, או 180° מצלעות שלהם. לכן כל קודקוד של כל משושה משותף עם עוד שני משושים נוספים, וחייבת להיווצר אותה תבנית תמיד.
האם יש אריחים שאפשר לרצף איתם את המישור אבל רק באופן לא מחזורי? עם יותר מאריח אחד, התשובה חיובית. הריצוף שמצא רוג'ר פנרוז אסתטי ואלגנטי, אבל יותר קל להיווכח בחוסר המחזוריות בריצופים שעסק בהם האו ואנג, בזכות הקשר לחישוביות. אריחי ואנג הם ריבועים שהצלעות שלהם צבעוניות, ומותר להצמיד שניים מהם זה לצד זה רק אם הצלעות תואמות. ניתן לממש את כלל ההתאמה הזה באופן גאומטרי שמוכר לכל מי שהרכיב פאזל, אבל יותר נוח לנתח את הריצופים עם המידע הקומבינטורי.
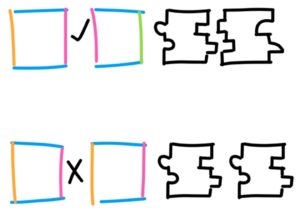
ואנג שיער שכל קבוצת אריחים שמרצפת את המישור, מרצפת אותו גם באופן מחזורי, בדומה לריבועים שאמנם יש להם ריצוף לא מחזורי אבל גם כן מחזורי. אם זה המצב אפשר להכריע אלגוריתמית אם האוסף מרצף את המישור או לא. הרעיון הוא להתחיל מאריח כלשהו, ולייצר את כל האפשרויות לשכנים שלו וכן הלאה. לאורך התהליך, או שמתישהו מגלים שאין אפשרות להמשיך את הריצוף, או שרואים מחזור באחת האפשרויות.
אבל במהרה מצאו קבוצות אריחים שאפשר לרצף איתן את המישור, ואין אף ריצוף מחזורי שעשוי מהן. איך בונים כזו? מתחילים ממכונת טורינג שרצה לנצח, ומקודדים אותה כאוטומט תאי חד-ממדי. אז התבניות שהאוטומט הזה יוצר הן תמיד לא מחזוריות. אפשר לקודד אוטומט תאי חד-ממדי באמצעות הצבעים: צבע בצד מעיד על התוכן של המשבצות השכנות, וצבע בצלע העליונה אומר לאיזה מצב האוטומט עובר. כל סידור של כלל התאים בעולם של האוטומט נותן ריצוף של המישור ולהיפך, ולכן אף ריצוף לא יהיה מחזורי. לאורך השנים מצאו עוד ועוד מודלים חישוביים שאפשר לקודד באריחים כאלה וכך מצאו קבוצות נוספות עם ריצוף לא מחזורי בלבד.
בסופו של דבר ג'ינדל וראו מצאו את קבוצת האריחים המינימלית שהיא לא מחזורית. אבל השימוש בצבעים ככלל ההתאמה היחיד די מגביל, ולראיה סוקולר וטיילור הציגו משושה עם כללי התאמה מורכבים, שיחד עם הסיבובים והשיקופים שלו אפשר לרצף את המישור, אבל רק לפי תבנית של משולש סירפינסקי, שהיא לא מחזורית. כללי ההתאמה הם לא רק צביעה, וכדי לממש אותם באופן גאומטרי האריח צריך להיות קבוצה לא קשירה. זה מעלה עוד שאלות: האם יש אריח קשיר שמרצף באופן לא מחזורי? ומה לגבי פחות סימטריות?
תוצאה בכיוון השני הגיעה בשנים האחרונות בריצופים של $\mathbb{Z}^2$. ריצוף מוגדר להיות אריח $A\subset\mathbb{Z}^2$ וקבוצת הזזות $T\subset\mathbb{Z}^2$ כך שהעותקים $ \{A + t : t \in T \}$ מכסים בדיוק את $\mathbb{Z}^2$, כלומר זה איחוד זר שלהם. בטאצ'רייה הוכיח שכל אריח כזה מרצף גם באופן מחזורי, ולכן שאלת הריצוף כריעה. הסיבוכיות של האלגוריתם תלויה באורך המחזור והמאמר הזה לא הציג חסם מדויק, ובהמשך גרינפלד וטאו פישטו את הטיעון וחסמו את הסיבוכיות לשאלה אם אריח מרצף את המישור הדיסקרטי בחסם מעריכי.

כל התוצאות חוץ מתכונת המחזוריות ב-$\mathbb{Z}^2$ הוכחו באמצעים דיסקרטיים: או בנייה של אלגוריתמים וגרפים, או טענות על מודלים חישוביים, או חיפוש במרחב האפשרויות. ההוכחה של התוצאה האחרונה שונה ומעניינת. את התכונה ש-$A$ מרצפת עם ההזזות $T$ ניתן לבטא באמצעות קונבולוציה $\mathbb{1} = \mathbb{1}_{-A} * \mathbb{1}_T$. התכונה הזו, בצירוף עם זה ש-$A$ סופית, מאפשרת למצוא בכלים אנליטיים פירוק
$$ \mathbb{1}_T(x) = \sum_{a \in A} \varphi_a(x) $$
כך שלכל $a \in A$, לפונקציה $\varphi_a:\mathbb{Z}^2\to[0,1]$ יש מחזור (בכיוון אחד). רוב ההוכחה עוסקת באיך למקד את הפונקציות $\varphi_a$ כך יקבלו ערכים יותר בדידים, עד שמגיעים לפונקציות שמקבלות רק את הערכים $0$ ו-$1$. זה שקול לקבוצת הזזות שהיא איחוד סופי של קבוצות עם מחזור בכיוון יחיד, והמשך ההוכחה ממצה מזו קבוצה מחזורית בשני כיוונים.
